This note is symbolic by design. It may not offer immediate utility to practitioners or digital finance observers, yet it points, I believe, to one of the most critically neglected dimensions in the design of digital money: topology. While much of the discourse circles around the local advantages of blockchain payment rails, or the specifics of reserve composition and its effects on value transfer across issuers and holders, very little attention is paid to the architecture that underlies it all. The shape of the network, the way value flows, the nature of monetary signal propagation. These are not secondary effects of the system—they are the system. The post below isn’t meant to be a scientific paper, but rather an invitation to raise the quality and rigour of the conversation. Because in the end, it is the topology of our money network that will determine who extracts value, how resilient the structure becomes, and what kind of monetary world we build on top of it.
Reflections On Monetary Network Topology
Money acquires its value from the network of mutual trust that surrounds it.
Effectively, trust imbues money with relatively efficient information, allowing it to compress messier, subjective perspectives on counterparties, goods, and services. If, from a financial perspective, money is some sort of deeply solvent credit instrument, from a mathematical one it can be treated as a shared signal. Money is part of a broader information system, compressing complex economic reality into a communicable signal that can travel through society’s networks with minimal friction.
We can picture an economic system as an enormous graph—where nodes represent people, applications, or financial institutions, and edges are channels of exchange. The signal flowing through the edges is significantly impacted by the interactions of all nodes; abrupt events across the network, like a sudden relative expansion or reduction of supply, or the disappearance of a certain number of nodes, can temporarily affect the quality of the signal until the shock is absorbed through the network. A topological theory of money should therefore treat money as a network phenomenon, where value (signal) is transmitted and continuously encoded/ decoded by all participants.
If money is a network phenomenon, then the design of the network (its topology) matters immensely. Let’s consider two extremes: a centralised star network and a distributed mesh network.
Centralised star network → In a star monetary topology, a central bank sits at the hub issuing base money (M0) to commercial banks, which then extend outwards to users. Centralised money is in some sense closed-source, given that ordinary users cannot independently verify its supply or rules, but decide to entrust the centralised authority that maintains them. We’ve grown so accustomed to this 20th-century form of money that regulatory compliance is now treated as absolute—an axiomatic good, where in truth it is merely a precondition: the satisfaction of a central authority that underwrites the system’s continuity. In this sense, compliance is not just legal or procedural. It’s epistemological. It defines what money is within a centrally-issued regime—an instrument whose validity emerges from alignment with the issuer’s power, not from its function in a broader network.

Distributed mesh network → Now consider a mesh or peer-to-peer network like Bitcoin’s, where each node can communicate with any other without a central intermediary. The value of a decentralised money network such as Bitcoin stems from network consensus and scarcity by design, and not from trust in a centralised authority. The topology of mesh networks is flat—or at most, has clusters but no single point of control. This is why Bitcoin maximalists aren’t animated by anarchism per se—they simply don’t see regulation as additive. In a system designed to propagate value through consensus rather than permission, the presence of a central authority contributes nothing to the information itself. Compliance, in this context, is noise. Authority doesn’t clarify the signal—it distorts it.

Network topology determines everything, including: how value accrual is distributed, what is the quality of the propagated signal, as well as its propagation efficiency.
Network Topology and Value Accrual
Unsurprisingly, value accrual in centralised designs tends to concentrate at the centre: the hub (central bank) enjoys a monopoly on issuance and can extract seigniorage—profit from creating money, and the spokes (commercial banks) benefit from being close to the source—cheap access to capital, and from the regulatory monopoly to lend it out. Liquidity in this network radiates from the centre: when the central hub adds money, all spokes receive the signal and money flows outward; when it tightens, all feel the squeeze.
In a mesh network like Bitcoin, instead, value accrues non-linearly from a time, rather than space, perspective. Early adopters and minters (those who contribute the initial energy required to push the system past its adoption escape velocity) are rewarded disproportionately. Their compensation is not solely for capital resources, but rather for initial belief and social coordination. As the network matures, late adopters enter a system where the hardest consensus work has already been done. They benefit from the emergent stability of distributed trust, not because they earned it, but because others did.
The following conjecture emerges over and over again from the analysis of network topology. Let G be a network with a defined topology T, and let A denote the corresponding value accrual function over the set of nodes V(G). We can conjecture that:
The structure T materially influences the distributional characteristics of A. That is, the topology of a network constrains the dynamics of value accrual within it—topology-dependent accrual
Conversely, a value accrual system A tends to stabilise and reinforce the network topology T that has enabled it—accrual-dependent topology stability
The implications of the conjecture are less than obvious. Any attempt to alter value distribution without modifying the underlying topology are structurally limited. Likewise, altering the network topology necessarily perturbs the embedded logic of value accrual. Topology and value distribution are, in other words, co-dependent and co-determined.
Signal Propagation Efficiency and Network Resilience
(Monetary) network topology affects how singular or fragmented signal (money) is. In an ideal structure, signal flows freely—fungible, interchangeable, and coherent across the network. This is the principle behind the singleness of money: one unit, universally accepted, moving without friction through the entire system. However, when a network breaks into sub-networks—silos or closed loops, fragmentation occurs: a dollar inside one closed payment system might not be exactly equivalent to a dollar in another at any point in time. Breakup into further sub-graphs can occur for several reasons: attempted value capture as well as throughput optimisation. Sub-monetary systems build fast lanes, clean APIs, neatly engineered stacks where money-as-signal moves fast—but only within bounded zones. These systems, however, remain frequently siloed, risking the fragmentation of monetary networks into isolated sub-graphs. It is a continuous tension: efficiency vs. singleness.

Stablecoins → Centrally-issued stablecoins are a revealing case and an interesting hybrid: a set of distributed mesh networks (often interconnected) and tied to a hierarchical one through isolated nodes operating based on different rules. The result is monetary fragmentation across competing technical and governance standards. During crypto’s early stages, such fragmentation was tolerable; the so-called crypto economy, whether off-chain speculation settled via stablecoins or early-stage DeFi primitives, remained peripheral to the core of the sovereign dollar system. The network topologies were separate enough that questions of signal integrity and monetary singleness could have been set aside. That separation, however, is quickly collapsing. As crypto-native dollars scale into broader economic use, the question of optimal macro topology becomes unavoidable. Practitioners and regulators alike must begin to treat it not as a technicality, but as a first-order design parameter.

While the rise of a digitally native dollar feels inevitable on technological grounds, regulators would do well to shift focus, from protectionism to the long-term topology of the monetary network. While the current trajectory, favouring large-scale issuers, might bring short-term efficiency, its long-term implications might well be different. From the perspective of a central monetary authority, this ossification might weaken monetary visibility and impair policy steering. From the perspective of application builders and final users, it could entrench extractive profit models and limit composability—which interestingly is what we have observed during the early phases of the crypto economy. Ironically, these financial architectures echo the very legacy structures crypto set out to escape from a computational perspective: proprietary meshes, permissioned interfaces, private rails masquerading as public goods.
A Macroprudential Approach To Monetary Topology
There is no singular trajectory for the evolution of digital money—only a contested field shaped by competing incentives. Regulators (should) aim for stability, incumbents seek to defend or cautiously extend profit centres, challengers are eager to carve out their share.
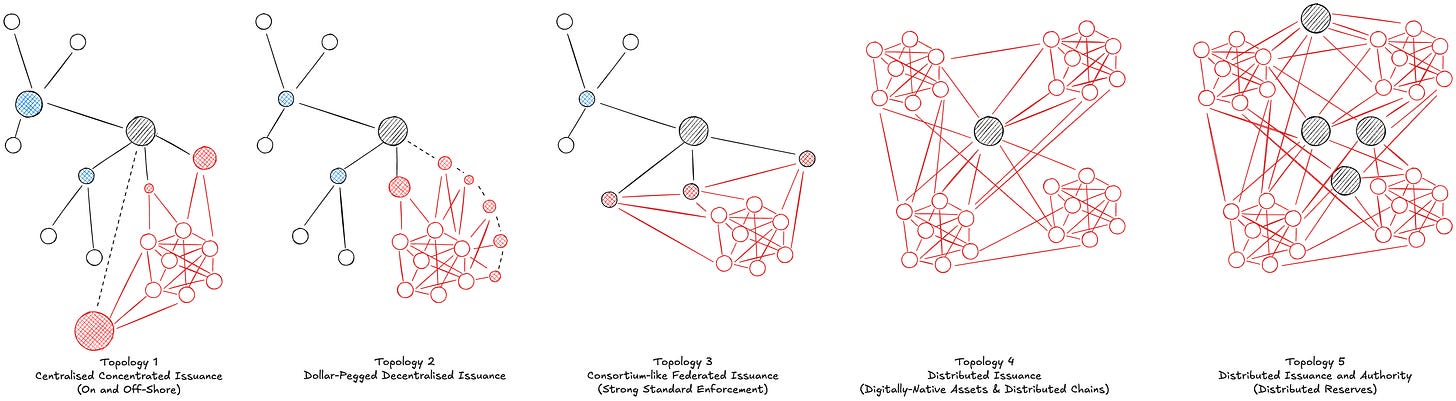
We can sketch a few alternative topologies for digital money to help our observations.
Topology 1 reflects the current dominant stablecoin market structure: a few regulated issuers act as gatekeepers to a mesh network, coexisting with a dominant unregulated issuer loosely tethered (…) to the monetary centre via the nature of the majority of its off-chain reserves and some support to enforcement actions. The result is degraded signal quality—due to fragmented standards, brittle network resilience—concentrated points of failure, and extreme value centralisation—see Tether’s margins. While this configuration expands the monetary use cases (more people and applications can access the dollar) and solves punctual frictions, its impacts on monetary stability cannot be disregarded.
Topology 2 maps to dollar-pegged, digitally native (but exogenously collateralised) currencies, like 2021-2024 $DAI. Connectivity to the core signal (the Fed, implicitly) is mediated through semi-official channels (think $USDC’s PSM or indirect US treasury exposure) and through rational, incentive-driven capital—mostly market makers. This improves resilience and softens value capture concentration versus Topology 1, but signal propagation remains lossy.
Topology 3 imagines a federated or consortium model—think Paxos’ Global Dollar or M0’s, though with distinct architectures. Here, a coordinated set of actors aligns around shared standards—regulatory in the case of Paxos and technical in M0’s framing. This boosts resilience and helps repair signal fidelity through protocol rules. Value accrual also shifts: Paxos shares the on-chain seigniorage across its issuers; M0 introduces an internal monetary policy, flexibly allocating incentives across the mesh in response to changing system needs.
Topology 4 is radical—and still further out. It envisions a flatter, more complex hybrid system: digital money issued organically, collateralised by digitally native assets, governed by contracts, and spread across multiple chains. In theory, this configuration maximises resilience and connectivity in a globally entangled world. Signal quality improves, central seigniorage can still be preserved—the US government still borrows cheap, but the surplus can be dynamically redistributed throughout the network. The logic of monetary value creation and capture is rewritten.
Topology 5 is the furthest frontier. Like Topology 4, it assumes a fully decentralised mesh. But here, there is no single source of authority—monetary signal originates from multiple centres. This is the architecture of basket-based digital monies, post-dollar in orientation, where value is indexed not to one sovereign but to a fluid basket of reference assets: digital and physical commodities, sovereign debt, tokenised credit and infrastructure, and who knows what else. Pegging becomes endogenous. Value is anchored internally, via dynamic equilibrium across the basket, not externally against a central source. Legitimacy comes not from state backing, but from embedded resilience and global usability. While it might take decades to achieve this, the outcome is in my opinion the most likely. At M0, we have designed protocol architecture to progressively evolve from Topology 3 to Topology 5 together with the broader economy, and to escape radically from Topology 1 which we consider an avoidable outcome.
The way monetary signal propagates can have dramatic economic and geopolitical effects. Each configuration, with its own topology, drives how value accrues across the system and how quickly (and resiliently) information can become coordination. While there is no universal blueprint, any serious stakeholder (public or private) must approach this through a macroprudential lens. Watch the flow, trace the signal, measure its fidelity, its velocity, and who captures what along the way.
Topology should no longer be a footnote, it needs to sit at the centre of how we think about monetary systems—especially now that we can observe them breathing in real time. Regulators, builders, and protocol designers alike can no longer afford to treat structure as incidental. The good news is quiet: the cat’s already out. Mesh networks are no longer speculative—they are technologically unavoidable. And that fact alone shifts the frame. Every time a topology locks value too tightly, every time centrality hardens into rent, the pressure builds. Quietly, persistently, structurally.
Appendix: a Graph-Theoretic Model of Monetary Network Topologies
The Appendix that follows intends to stimulate discussion over the creation of a formal graph-theoretic model to evaluate monetary network topologies. We can think about it as a first step towards a more scientific, paper-like, publication that formalises what we have discussed qualitatively above.
In this formalism, we represent a monetary network as a graph G(V,E) where nodes V are entities or users and edges E represent direct monetary connections. We focus on three key evaluation dimensions for such a network: (1) Value Extraction Capacity, (2) Signal Communication Quality, and (3) Resilience:
Value Extraction Capacity is the theoretical ability of actors/ to extract rent from the network’s periphery. In graph terms, this relates to centrality measures (e.g. degree and betweenness) which quantify a node’s importance or control over network flows. A highly centralised topology (one or few hubs) may enable those hubs to impose fees or policies unilaterally on others
Signal Communication Quality is the efficiency and fidelity of information (price signals, policy changes) transmission across the network. This dimension relates to the network’s connectivity and coherence–whether it behaves as a single integrated monetary zone, and can be quantified by metrics like path length, diameter, and spectral properties (e.g. the algebraic connectivity or eigenvalue gap) that govern consensus or diffusion speed. A more coherent network (single component, short paths) should converge on one price level and liquidity pool more readily
Resilience is the robustness of the monetary network to failures, shocks, or attacks—e.g. censorship. This corresponds to redundant connectivity: multiple alternative paths and absence of single points of failure. Graph metrics can include vertex/ edge connectivity—minimum nodes or links whose removal disconnects the graph, clustering—cycles, and algebraic connectivity (Fiedler eigenvalue) which provides a spectral measure of robustness. High Resilience means the network can route around shocks, maintaining operation even if some nodes are removed
Using this framework, we can classify idealised monetary network topologies (from highly centralised star configurations to decentralised meshes) and evaluate each type against these three dimensions. We could also propose composite indexes (some sort of Monetary Network Integrity Score) that combine all dimensions, and argue that increasing effective decentralisation (toward a mesh topology) maximises overall integrity.
To ground our analysis, we should then follow to outline graph-theoretic metrics connecting topology to each of the three dimensions described above.
Degree of Distribution and Centralisation
Each node v has degree d(v), representing the number of edges (connections) it has. The degree distribution P(k) describes how connectivity is spread among nodes. Highly unequal degree distribution (a few nodes with very large degree, many with small degree) indicates a hub-and-spoke structure like our central banking depiction above. We can quantify overall network centralisation using Freeman’s centralisation index, which sums the differences between the highest-degree node and all others. A star network, for instance, achieves maximum degree centralisation: one hub connected to N-1 others. High centralisation often implies greater capacity for the hub to control or extract value from flows. In particular, a hub with high degree and betweenness can act as a toll collector for transactions. Betweenness centrality Cb(v) is defined as the fraction of shortest paths between all other node pairs (s,t) that pass through v. Formally:
where sigma is the total number of shortest paths from node s to t, and sigma(v) is the number of those paths that go through v. A node with high betweenness centrality lies on many shortest routes and can thus mediate exchanges between others. Betweenness is a measure of others’ dependence on a given node, and therefore a measure of potential control.
In economic terms, a monopolistic intermediary could charge rent on flows it brokers; models of trading networks show that intermediaries’ payoffs can be proportional to their betweenness centrality. Thus, we associate Value Extraction Capacity with centralisation: networks with one or few nodes having outsized degree or betweenness indicate high potential for rent extraction by those nodes, whereas a decentralised graph (no critical hubs) limits unilateral rent-seeking. It is unsurprising that large centralised stablecoin issuers like Circle and Tether are pitching the importance of their market position to the regulator to avoid losing it—interestingly it doesn’t seem the regulator is always listening to them.
Path Length, Diameter, and Signal Propagation
The efficiency of information or value transfer is tied to graph distances. The shortest path length between two nodes (geodesic distance) indicates how many hops are required for a transaction or message to travel. In a well-integrated monetary network, distances are small; in other words the diameter (max distance between any two nodes) and average path length are low—so that price signals or liquidity shocks propagate quickly to all participants. For example, a star system has diameter 2—every node is at most one hop from the hub and two hops from any other node via the hub, whereas a linear chain or poorly connected clusters have larger distances. Spectral graph theory provides a more nuanced handle on information flow, but it is beyond the scope of this Appendix. Intuitively, graphs with higher connectivity and shorter paths let information converge more quickly, as confirmed in small-world network studies: introducing shortcut links dramatically enhances signal propagation and global coordination by reducing path lengths. We can use metrics like average shortest path and algebraic connectivity as proxies for Signal Communication Quality—higher values correspond to more unified price information (the famous singleness of money) across the network. The persistence of centralising large intermediaries is antithetic to the natural evolution of networks of enhanced communication quality.
Connectivity, Clustering, and Resilience
Resilience is captured by how many independent paths connect the network. A network’s node connectivity k(G) is the minimum number of vertices whose removal disconnects G, and similarly edge connectivity lambda(G) is the minimum edges whose removal disconnects the graph. These metrics directly measure robustness: the larger k(G) is, the more failures the network can absorb while still remaining whole. Equivalently, high connectivity means there are multiple disjoint paths between any two nodes. A classic result is that algebraic connectivity provides a lower bound on node and edge connectivity, so a larger Fiedler value implies a more robust network. Another measure of redundancy is the presence of cycles—captured by the clustering coefficient or the count of alternative loops in the graph. A cycle means there’s an alternate route between nodes. For example, a triangle (3-cycle) provides each node two distinct paths to reach the third. Densely clustered networks with many loops have high redundancy, whereas a tree (no cycles) has exactly one path between any two nodes—no redundancy. Resilience also ties to assortativity, i.e. whether high-degree nodes tend to connect to other high-degree nodes. A decentralised mesh often shows some connectivity among major nodes, preventing any single hub from being irreplaceable. In contrast, a strict star or hierarchical network is often disassortative—high-degree hub connected only to low-degree leaves, which makes the hub an obvious single point of failure. Overall, we can evaluate resilience by considering connectivity—minimum cut sizes, spectral gap, and redundancy metrics. A robust monetary network is one where no single node (or small set) can fatally compromise the system; it routes around failures via multiple redundant paths.
Application to Cases With Centralised Stablecoin Issuers on Decentralised Ledgers
Today’s dominant hybrid monetary networks combine a centralised issuance with a decentralised transaction network. Prime examples are centralised stablecoin issuers such as Circle’s or Tether’s, where the circulating supply is tailored to exist on public blockchains. Topologically, this system can be modelled with two layers:
A trust layer where the issuer is a central authority hub—all tokens are a claim on that issuer
A transaction layer where users (token holders) can directly transfer tokens among themselves over a peer-to-peer network—the blockchain, without routing through the issuer for each payment
In graph terms, we can draw the trust layer with an edge that goes from the issuer to all users, representing the issuer’s ability to affect each account, e.g. freeze or redeem tokens. Separately, we can describe the transaction layer drawing user-to-user edges for actual payment channels on the blockchain, where users form a mesh or at least a well-connected graph. This hybrid structure leads to unique properties.
Value Extraction Capacity in this system lies primarily with the central issuer, albeit in different form than transaction tolls. The issuer can extract value through seigniorage or control of the monetary base—much like a central bank. For example, the stablecoin issuer can earn interest on reserves, charge fees for redemption, or potentially freeze and confiscate tokens—which is an extraction of value from the holder. The issuer’s centrality in the trust graph is absolute: every token depends on the issuer’s backing. However, the issuer’s betweenness centrality in the transaction graph is minimal, because users don’t have to route payments via the issuer. If we consider the flow of transactions as the network, the issuer is not on the shortest path between users who transact directly. Thus, unlike a pure star, the issuer here cannot levy a fee on every transaction by architecture—users send value P2P on the blockchain. This reduces traditional rent-extraction via transaction fees. Instead, the issuer’s power is more off-chain: they can change the rules of redemption or supply. In graph terms, the issuer has degree N—it is connected to all users accounts in terms of oversight, but zero betweenness for user-user shortest paths—since it’s not needed to connect them. This paradoxical mix means some forms of extraction are curtailed—no mandatory transaction tolls, yet others remain—central control of asset validity. From a trust layer perspective, the issuer is a single point of authority, the ability to enact centralised policy enforcement impacts a peripheral node’s connectivity. For this reason, the issuer can (and will) exert rent extraction or censorship unilaterally on a given address—a power analogous to a central bank freezing assets. From a practical view, if this stablecoin dominates the monetary network, as in the case of Tether or to a lesser extent Circle, the issuer could impose fees or negative interest on all tokens globally, a form of rent extraction at scale. Value extraction capacity remains high at the point of issuance, even if day-to-day user payments appear decentralised. This is where technical smart-contract design becomes an important detail.
Signal Communication Quality in the hybrid network is typically excellent, thanks to the underlying blockchain connectivity. All users share a common ledger, meaning the state (balances, recent transactions, etc.) is visible to all and updated globally with each block. In Bitcoin or Ethereum P2P networks, the diameter is small—on the order of 4–6 hops across the globe, given the small-world properties of the Internet. Thus, payment signals (transactions) and price information diffuse quickly among users. Furthermore, since a centrally-issued stablecoin would be by definition the same everywhere, improving singleness of money within the system. The spectral gap of the P2P network ensures robust synchronisation—information entropy decays as messages mix and reach all nodes. In sum, signal quality is high: the network behaves as a unified ledger with fast propagation. All participants essentially share the same broadcast channel for ledger updates, ensuring that liquidity and price signals are globally coherent. There is, however, a nuance: the quality of the value signal (the stablecoin’s peg to fiat alternative) depends on off-chain trust, or better connectivity between the single issuer and the rest of the fiat system. This is where a holistic topological analysis of the broader monetary network is required.
The model shows an interesting dichotomy when it comes to Resilience. Quantitatively, the graph connectivity of the user network appears high—perhaps k(G) is large, but if we include the issuer node with edges to all, removing that node doesn’t disconnect the graph topologically, yet it disconnects them from the central source of trust. We might therefore need to formalise issuer connectivity as a special metric: if the issuer node is removed along with all its edges, do the remaining nodes still have value connectivity? While nodes can still reach each other—so pure graph connectivity is preserved, the information they exchange may be worthless given that there is no redemption path. In effect, the issuer node acts as an ultimate backstop. Such a hybrid would score very high on network robustness (censorship resistance of transactions via decentralisation) but extremely low on control robustness—one entity controls monetary policy and can be pressured.
In summary, users pay an often-enormous value extraction fee to the centralised issuer for the benefit of fast transaction during normal times, while the central monetary authority (i.e. the regulator) is ultimately worse off by losing control over monetary policy, at the expense of a more fragile economy, and in the sole interest of the transaction benefit of the ultimate users. Ironically, or sadly, distributed ledger technology was born to start swinging the pendulum towards less intermediated yet less efficient networks that could sustain dramatic shocks and avoid disproportionate rent seeking, the sadness of those trying to pitch centralised efficiency in the context of decentralised network is not lost in me.







It sounds to me like a complementary analysis that would live on top of the graph is understanding information dynamics. Cybernetic instead of topological analysis.
In essence, you are defining the graph, but you should add rules for transition and flow on top of that graph and investigate the dynamics of flow through the graph instead of just positing certain topologies correspond with certain final steady states.
An example would be defining some graph and then a Markov process on top of it and studying the master equation (or approximate Fokker-Planck equation) of that graph.
This would give timescales for information to propagate, and timescales for credit expansion/contraction.
Sounds fun to look at in a toy context!
thank you it's dirt